Short description

This code serves as a diagnostic tool to check that symmetry heuristics are working as they should. The code prints which Bravais lattice was identified, which high symmetry points in the BZ are inequivalent, and so on. The Brillouin zone and its irreducible wedges are printed to files as polyhedra for manual inspection, and the symmetry operations of the lattice can be printed.

Command line options:

Optional switches:

• --printsymmetry
  default value .false.
  Also prints the symmetry operations

• --help, -h
  Print this help message

• --version, -v
  Print version

Examples

crystal_structure_info

crystal_structure_info --printsymmetry

Long summary

This is mainly a diagnostic tool, to make sure that my heuristics are working as they should. For example, if you want to calculate fcc Al, and things look strange, run this code to make sure that the symmetry detection actually identifies it as fcc. As a bonus, the Brillouin zone and the irreducible wedge is printed to file, so that you can make figures like the one below.

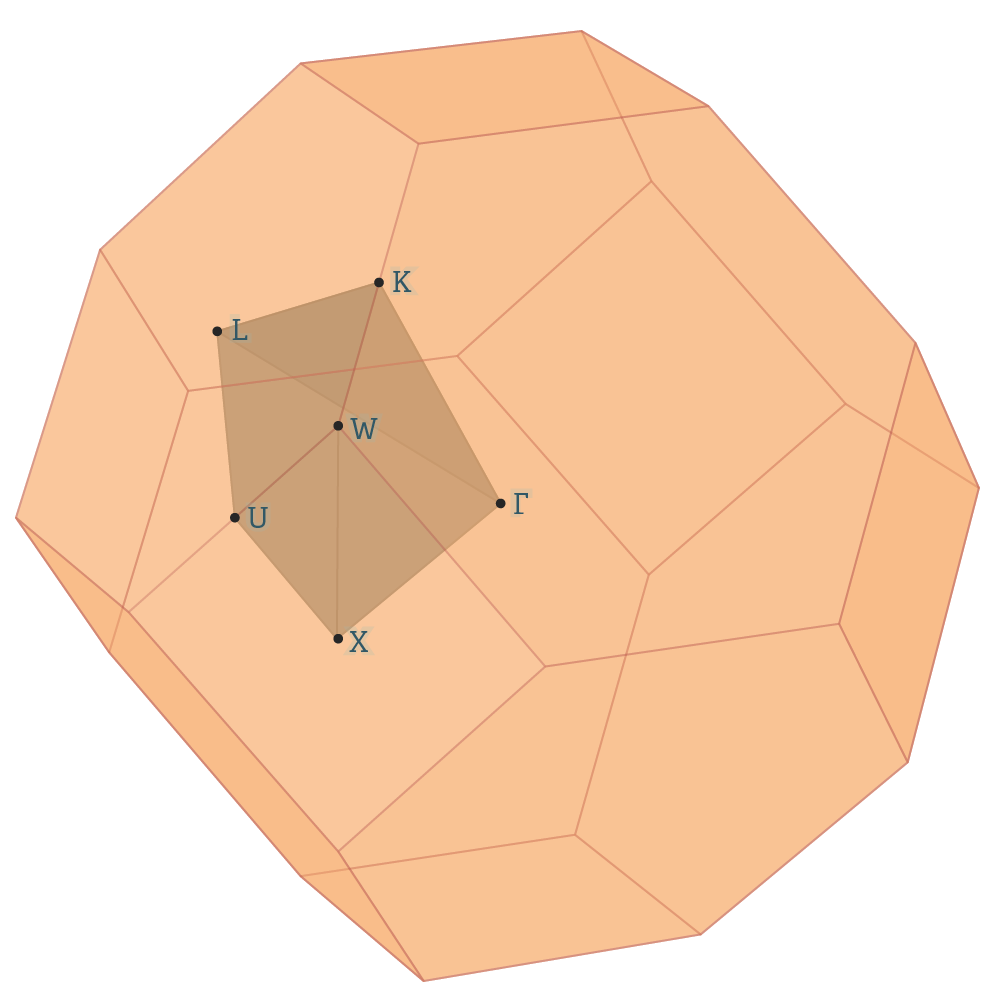
Input files

• infile.ucposcar

Output files

outfile.brillouin_zone.hdf5

This contains the information to produce the plot above. I did it with the following matlab snippet:

% read all the stuff
fn='outfile.brillouin_zone.hdf5';
zone_nodes=h5read(fn,'/zone_nodes')';
wedge_nodes=h5read(fn,'/wedge_nodes')';
nf=h5readatt(fn,'/','number_of_zone_faces');
for i=1:nf
    zone_faces{i}=h5read(fn,['/zone_face_' num2str(i)]);
end
nf=h5readatt(fn,'/','number_of_wedge_faces');
for i=1:nf
    wedge_faces{i}=h5read(fn,['/wedge_face_' num2str(i)]);
end
labels=strsplit(h5readatt(fn,'/','wedge_node_labels'));

figure(1); clf; hold on; axis equal off; view(3); camlight;
    i=drawPolyhedron(zone_nodes,zone_faces);
    set(i,'facealpha',0.3)
    j=drawPolyhedron(wedge_nodes,wedge_faces);
    set(j,'facealpha',0.3,'facecolor','blue')
    for i=1:length(labels)
        text(wedge_nodes(i,1),wedge_nodes(i,2),wedge_nodes(i,3),labels{i})
    end

This requires the Geom3D package.

outfile.qpoints_dispersion

This is a prototype version of infile.qpoints_dispersion, so that you don't have to start from nothing when changin the path. It can look like this:

FCC                         ! Bravais lattice type
  100                       ! Number of points on each path
    4                       ! Number paths between special points
GM  X                       ! Starting and ending special point
X   U                       !
K   GM                      !
GM  L                       !

It might not agree with my canonical form.

Find the primitive cell

reduce a set of lattice vectors to canonical form